Der Dreisatz ist ein intuitives Lösungsverfahren für Proportionalaufgaben: Mit dem Online Dreisatz Rechner oder der Excel Dreisatz Version löst Du diese Textaufgaben im Handumdrehen! Er wird auch als Verhältnisgleichung, Schlussrechnung oder Proportionalitätsrechnung bezeichnet. Aus drei bekannten Werten kann auf sehr einfache Art der unbekannte vierte Wert bestimmt werden – daher der Name.
Die Berechnung erfolgt ganz einfach, du brauchst dafür keine Formeln auswendig zu lernen: Du schreibst die 3 Werte in 2 Spalten an und rechnest in beiden Spalten immer das gleiche.
Downloads und Beispiele
Das Lösen von Textaufgaben bereitet oft große Schwierigkeiten! Der Dreisatz ist aber ein ganz einfaches und leicht zu automatisierendes und zu Erlernendes Werkzeug und ist bestens geeignet für eine Excel Berechnung. Unter den folgenden Downloads findest du einige Dreisatzaufgaben mit Lösungen und Beispielen zum selber ausprobieren. Viel Spaß!
- Beispiele und Lösungen – Exceltabelle zum einfachen und umgekehrten Dreisatz
- Zusammenfassung als PDF-Datei
- Online 3 Satz Rechner zum schnellen Üben (siehe unten)
Dreisatz Formel
Wenn alle folgenden 3 Punkte eingehalten werden, kann der Dreisatz in seiner klassischen Form angewendet werden.
- Es müssen genau 3 Angaben im Text stehen (A1, A2, B1)
- Zwei Angaben davon müssen artgleich sein (A1, A2)
- Ich kann den Text umformulieren: je mehr, desto mehr(A1:A2=B1:X) oder desto weniger (A1:A2=X:B1)
Wenn nun diese beiden Formeln nach X aufgelöst werden ergibt sich die Dreisatz Formel für den
- proportionalen Fall: X=A1/A2*B2
- antiproportionalen Fall: X=A1/A2*B2
Das war jetzt viel Theorie, am einfachsten erklärt sich das ganze anhand eines einfachen Beispiels:
das Schokolade-Massaker 🙂
Das Schokolade Beispiel Teil 1 (proportionaler Dreisatz)
Regel für den proportionalen Dreisatz:
je mehr – desto mehr
je weniger – desto weniger
Grundsätzlich darf der Dreisatz nur verwendet, werden wenn ein proportionaler Zusammenhang vorliegt. Ein proportionaler Zusammenhang liegt vor, wenn ich sagen darf: je mehr Riegel Schokolade ich esse, desto mehr Kilogramm werde ich zunehmen 😉
Ich habe also 80 Riegel Schokolade. Und ich weiß, dass ich von 12 Riegel Schokolade ca. 300 g zunehmen. Wie viel nehme ich zu wenig die ganze Schokolade fresse?
Das ist eine typische Dreisatzaufgabe: da ist auf der einen Seite die Schokolade und auf der anderen Seite bin ich mit meinem Gewicht. Von der einen Seite weiß ich 2 Sachen (12 Riegel bzw. 80 Riegel), von der anderen Seite weiß ich nur eine Sache (300 g).
Diese Tabelle kann mathematisch auch mit der Dreisatzformel geschrieben werden:
- A1/A2 = B1/B2 … 12/80 = 300 / X
Diese Gleichung nach X umgeformt ergibt schon die Lösung:
- X=80/12*300=2000 Gramm
Ich werde also satte 2 Kilo zunehmen, wenn ich die ganzen 80 Schokoriegel alleine esse. An dieser Stelle wird die Sache jetzt aber interessanter: denn neben dem proportionalen Dreisatz gibt es auch noch den sogenannten antiproportionalen Dreisatz! Dieser entsteht beispielsweise bei folgendem Schokoladen Problem:
Das Schokolade Beispiel Teil 2 (antiproportionaler Dreisatz)
Regel für den antiproportionalen Dreisatz:
je mehr – desto weniger
je weniger – desto mehr
Ich habe also einen ganzen großen Berg Schokolade. Ich bin aller schnellsten imstande meine ganze Schokolade in 45 Minuten zu essen. Wie lange überlebt nun der Schokolade-Haufen, wenn Tante Erna, der kleine Francesco und ich gleichzeitig versuchen, die ganze Schokolade ratzeputz zu verschmachten?
Grundsätzlich handelt es sich hier wieder um den klassischen Dreisatz: da ist auf der einen Seite wieder die Schokolade und diesmal auf der anderen Seite die Anzahl der hungrigen Esser. Von der einen Seite weiß ich 2 Sachen (1 Person bzw. 3 Personen), von der anderen Seite weiß ich nur eine Sache (10 Minuten). Nun sagt mir der Hausverstand: je mehr hungrige Esser da sind desto weniger Zeit, also desto kürzer, wird die Schokolade überleben. In diesem Fall heißt es also nicht je mehr… desto mehr sondern: je mehr… desto weniger. Genau das ist ein antiproportionaler Dreisatz! Die Lösung erfolgt in ähnlicher Weise.
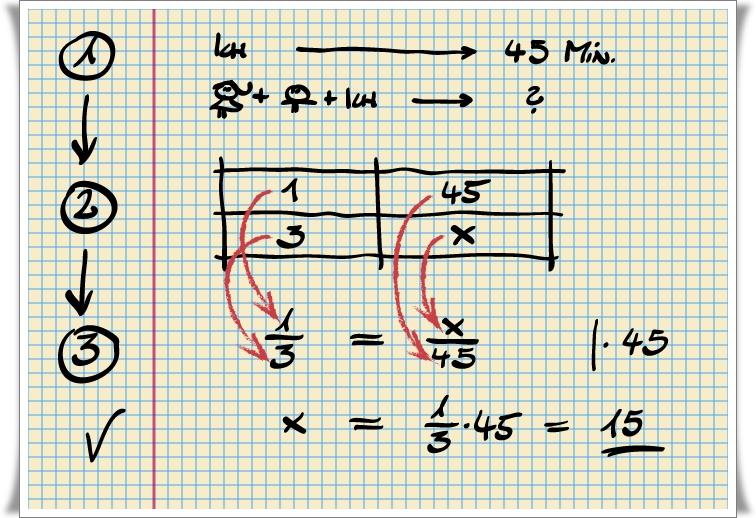
Diese Tabelle kann in die Dreisatzformel umgewandelt werden:
- A1/A2 = B2/B1 . 1/3=X/45
Beachte, dass hier die antiproportionalen Formel zum Einsatz kommt.
Diese Gleichung nach X aufgelöst ergibt bereits die Lösung:
- X=1/3*45=15 Minuten
Wir 3 werden also die gesamte Schokolade in einer Viertelstunde verputzt haben! Das ist eine feine Sache! Zu beachten ist das im oberen Beispiel ein kleiner Stolperstein eingebaut war: es wird oben von 80 Schokoriegel angesprochen.
Dreisatzaufgaben
Die folgenden Aufgaben inklusive den zugehörigen Lösungen sind alle als Excel Version kostenlos zum Downloaden bereitgestellt. Alternativ kannst Du mit dem gut erläuterten Online 3 Satz Rechner (siehe unten) auch gleich Deine eigenen Berechnungen sofort durchführen!
- Peter sammelt in 56 Minuten 7 Kilo Äpfel. Wie lange braucht Peter, um 25 Kilo Äpfel zu sammeln?
- Eine Schnecke legt in 5 Stunden und 32 Minuten einen Gewaltmarsch von 83 cm zurück. Wie lange brauchte sie, um quer über Kurtchens Schreibtisch zu marschieren, der eine Diagonale von 112 cm hat?
- Für 3 Gläser Erdbeermarmelade braucht man 5,1 kg Walderdbeeren. Herr Moritz möchte seiner Nachbarin 17 Gläser Erdbeermarmelade schenken. Wie viel Kilogramm Wald Erdbeeren muss er pflücken?
- Wenn Herr Moritz zum pflücken von genau 1,7 kg Walderdbeeren 56 Minuten benötigt, wie lange braucht er wenn er seine 7 Freunde bittet, ihm beim sammeln zu helfen?
- 3 Maulwürfe fressen in meinem Garten täglich 870 Regenwürmer. Einer der Maulwürfe wandert in den Garten meines Nachbarn. Wie viele Regenwürmer werden jetzt in meinem Garten gefressen?
- Mein Gehirn ist zu einem Fünftel mit Flausen gefüllt. Meine gesamte Gehirnmasse beträgt genau 3,5 Liter. Wie viel Liter Flausen sind in meinem Gehirn?
Die Auflösung:
Überlege dir ob es überhaupt eine Dreisatz-Anwendung ist (siehe Kapitel Dreisatz Formel) und belege die einzelnen Angaben mit den Werten A1, A2, B1 und B2 bzw. X. Überlege, ob es ein proportionaler oder ein antiproportionaler Fall ist. Fertig, wenn du die entsprechende Formel an!
Die Auflösung zu den oben angeführten Beispielen findest du im Downloadbereich. Dort kannst du selbst mithilfe der Excel Tabellen verschiedene Varianten und Ideen ausprobieren und herausfinden ob auch du irgendwelche Flausen im Kopf fast 😉
Dreisatzrechner online
Zur schnellen Überprüfung findest du hier auch noch einen Online Rechner. Mit dieser Hilfe kannst du schnell numerische Werte ermitteln, eigene Dreisatzaufgaben zusammenstellen oder Lösungen für deine Hausaufgaben finden. Ich empfehle dir aber, die Excel Tabellen von oben zu verwenden. Sie sind wesentlich übersichtlicher und mit ihrer Hilfe kannst du die ganze Dreisatz-Problematik wesentlich besser verstehen und verdeutlichen! Aber nichtsdestotrotz – hier die schnelle Lösung:
3 Satz Rechner mit Excel
Die Tabellenkalkulation Excel ist wie geschaffen für die Berechnung des Dreisatzes. Im Grunde ist dies ja nichts anderes, als eine Tabellenkalkulation, die du im vorliegenden Fall in der Regel mit der Hand löst. Das muss aber nicht sein, Excel rechnet für dich und so werden aus allen Dreisatzaufgaben Lösungen in Windeseile zusammengestellt.
Der Dreisatzrechner kann in unterschiedlichsten Varianten realisiert werden. Im Downloadbereich oben kannst du verschiedene Versionen kostenlos herunterladen. Mit diesen Werkzeugen bist imstande fast alle Textaufgaben in Windeseile, einfach und übersichtlich zu lösen.
Weiterführende Links
Hier gäbe es noch viel zum Erzählen und Probieren. Wenn Du Interesse Hast, das Thema noch weiter zu vertiefen, kann ich Dir diese Homepage wärmsten weiterempfehlen: Du findest fort neben vielen gut sortieren Beispielen und Übungen Hintergundwissen, atlernative Berechnungskonzepte, Infos zur Entwicklung und Geschichte sowie zahlreiche Tipps: